From cooking to budgeting, fractions are everywhere. Our guide breaks down the process into simple, relatable steps. Let's turn fractions from a mystery into a tool you can use every day!

Understanding Fractions: The Basics
At its core, a fraction represents a part of a whole. It's composed of two numbers: the numerator, located above the line, and the denominator, below the line. The numerator indicates how many parts of the whole you have, while the denominator tells you how many parts the whole is divided into.
For example: in the fraction 1/2, the numerator 1 signifies one part of the whole that's split into two, indicated by the denominator 2.
Types of Fractions
- Proper Fractions: The numerator is smaller than the denominator, such as
1/2 or 2/3. These fractions represent less than one whole. - Improper Fractions: The numerator is greater than or equal to the denominator, like
5/4. These represent an amount greater than one whole. These can be converted into mixed numbers for easier understanding. - Mixed Numbers: These combine a whole number with a fraction, showing amounts greater than one, such as
1 3/4.
Step by Step: How To Add Fractions
Navigating through the realm of fractions can seem daunting at first, but with a step-by-step approach, adding fractions becomes a breeze. In the upcoming sections, we'll break down the process for adding fractions with the same and different denominators, as well as mixed numbers, into simple, manageable steps to ensure you grasp each concept with ease and confidence. Let’s go!
Adding Fractions with the Same Denominator
Adding fractions might seem a bit like trying to mix oil and water at first glance, but once you get the hang of it, you'll see it's more like blending your favourite smoothie - smooth and straightforward, especially when the denominators are the same.
Let's dive into the simple steps that make adding such fractions as easy as pie (or should we say, as easy as adding slices of pie!).
- Step 1: Check the Denominators: Ensure that the fractions you are adding have the same denominator. This tells you they're divided into the same number of parts, making them ready to combine.
- Step 2: Add the Numerators: Simply add the numerators and keep the denominator the same. This is how many parts you have in total now.
- Step 3: Simplify if Necessary: Sometimes your answer can be reduced to a simpler form. Keep an eye out in the question to see if you’re asked to do this or if it’s easier to represent the fraction this way.
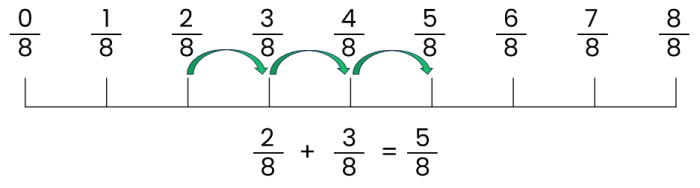
Example:
Let's add 2/8 and 3/8.
Both fractions have the same denominator (8), so we're good to go.
Add the numerators: 2 + 3 = 5.
Because the numerators are the same, we don’t need to change it.
Our answer is 5/8.
You can also imagine you and a friend have slices of the same pizza which has been cut into 8 slices. You have two slices of it 2/8, and your friend offers you their three slices 3/8. Combine the slices, and voila, you have five slices out of the total of 8 slices - 5/8 of a whole pizza.
Try it for yourself!
-
Add 1/4 + 2/4
-
Add 3/8 + 5/8
Solutions
- 1/4 + 2/4 = 3/4. The denominators are the same, so we just add the numerators: 1 + 2 = 3. The fraction is already in its simplest form.
- 3/8 + 5/8 = 8/8 or 1. Again, with the same denominators, we just add the numerators: 3 + 5 = 8. Since 8/8 is equivalent to 1, the answer is 1 whole.
Feeling more confident? Fantastic! To get even more practise and reinforce what you've learned, check out our worksheet on adding fractions with the same denominators. It's packed with exercises designed to turn you into a fraction-adding wizard in no time.
Remember, every fraction adds up to your growing maths skills, and with each step, you're piecing together a bigger picture of mathematical understanding. Keep practising, and soon, adding any fractions will feel like second nature.
Adding Fractions with Different Denominators
When fractions have different denominators, it’s a little tricker. Before when the denominators were the same, it was really easy, so essentially, that’s what we’re trying to achieve here! The key to adding them is to make the denominators the same, known as finding the lowest common denominator (LCD). This process ensures that the fractions are speaking the same mathematical language, making addition straightforward and simple. Let's dive into how to navigate this essential skill with a step-by-step guide.
Finding the Lowest Common Denominator (LCD)
- Identify the Denominators: Look at the denominators of the fractions you need to add. For example, if you're adding 1/3 and 2/5, your denominators are 3 and 5.
- Find the Lowest Common Multiple (LCM): We need to look at the times tables for both of these denominators and find the lowest multiple they have in common. Which number is in both times tables? For 3 and 5, they both have 15 in their times tables. There are other numbers but this is the lowest. 15 is the LCM so will be our LCD.
- Adjust the Fractions: Convert each fraction to an equivalent fraction with the LCD as the new denominator. To do this, multiply the denominator to turn it into the LCD, in this case 15. So, for 1/3 we want 3 x 5 = 15. We now need to multiply the numerator by the same amount. Remember: ‘What you do to the bottom number, you must do to the top!’ So, for 1/3 we want 1 x 5 = 5. This gives us an answer of 5/15. We then do the same to the other fraction then add them.
If you need more help finding the LCD, take a look at our worksheet on common denominators.
Step-by-Step Guide to Adding
Using our example of 1/3 + 2/5
- Step 1: Find the LCM: We look at the times tables of 3 and 5 and find the 15 is the lowest common multiple.
- Convert to Equivalent Fractions:
- To convert 1/3
- Denominator: 3 x 5 = 15
- Numerator: 1 x 5 = 5
- Answer = 5/15
- To convert 2/5
- Denominator: 5 x 3 = 15
- Numerator: 2 x 3 = 6
- Answer = 6/15
- To convert 1/3
- Step 2: Add the Fractions: Now that both fractions have the same denominator (15), simply add the numerators:
- 5/15 + 6/15 = 11/15
- Step 3: Simplify if Necessary: If the fraction can be simplified, do so. In our case, 11/15 is already in its simplest form.
Now try some for yourself…
- Add 1/4 and 2/8.
- Add 1/2 and 2/5.
Solutions
- 1/4 + 2/8 = 1/2. The LCD of 4 and 8 is 4, so you can just convert 2/8 to its simplest form, 1/4. This makes it 1/4 + 1/4 = 2/4, which simplifies to 1/2.
- 1/2 + 2/5 = 5/10 + 4/10 = 9/10.
Step by Step: Adding Mixed Numbers
Mixed numbers are a blend of whole numbers and fractions, representing quantities greater than one. Adding them might seem like juggling apples and oranges at first, but with a straightforward process, it's as easy as pie. Let's slice through this mathematical challenge together, transforming mixed numbers into improper fractions, adding them up, and then neatly converting them back.
Converting Mixed Numbers to Improper Fractions
- Step 1: Multiply the Whole Number by the Denominator: Take the whole number part of the mixed number and multiply it by the denominator of the fraction part.
- Step 2: Add the Numerator: To the product, add the numerator of the fraction part.
- Step 3: Write as a Fraction: The sum becomes the numerator and you keep the original denominator to get your improper fraction.
Example:
Convert 3 2/5 to an improper fraction.
Multiply the Whole Number by the Denominator:
3 x 5 = 15
Add the Numerator:
15 + 2 = 17
Write as a Fraction:
The sum becomes the numerator with the original denominator to get 17/5.
So, the mixed number 3 2/5 converts to the improper fraction 17/5.
Adding Improper Fractions
With your mixed numbers now in the form of improper fractions (where the numerator is larger than the denominator), you simply add them as you would with any fractions, ensuring you have a common denominator first.
For example, 17/5 + 6/5 would simply become 23/5.
Converting the Result Back to a Mixed Number
- Divide the Numerator by the Denominator: This will give you the whole number part of your mixed number.
- The Remainder Becomes the New Numerator: Place this over the original denominator to form the fractional part of your mixed number.
Let’s use our previous example:
23/5
If we divide the numerator by the denominator, 23 divided by 5, we get 4 with 3 remainders so 3/5 left over.
Therefore, 23/5 becomes 4 3/5.
Now give these a try:
- Add 1 1/2 and 2 2/3.
- Add 2 1/3 and 3 1/4.
Solutions
- 1 1/2 add 2 2/3 = 4 1/6. Convert to improper fractions: 3/2 and 8/3. Find a common denominator (6), giving 9/6 and 16/6. Add them to get 25/6, which converts back to 4 1/6.
- 2 1/3 add 3 1/4 = 5 7/12. Convert to improper fractions: 7/3 and 13/4. Find a common denominator (12), giving 28/12 and 39/12. Add them to get 67/12, which converts back to 5 7/12.
Test Your Skills
- Add 1/8 + 3/8.
- Add 2/3 + 5/6.
- Add 1 1/4 + 2 3/4.
- Add 7/10 + 2/5.
- Add 3 1/2 + 2 2/3.
Solutions
- 1/8 + 3/8 = 4/8, which simplifies to 1/2.
- To add 2/3 and 5/6, convert to a common denominator of 6, giving 4/6 + 5/6 = 9/6, which we can convert to 1 1/2.
- Convert mixed numbers to improper fractions, giving 5/4 + 11/4 = 16/4, which simplifies to 4.
- Convert 7/10 and 2/5 to a common denominator of 10, resulting in 7/10 + 4/10 = 11/10, which is an improper fraction equal to 1 1/10.
- Convert to improper fractions, resulting in 7/2 + 8/3. Finding a common denominator of 6, we get 21/6 + 16/6 = 37/6, which simplifies to 6 1/6.
As we wrap up our fraction-filled journey, it's clear that mastering the addition of fractions is a critical skill that opens up a world of problem-solving and analytical thinking, essential both in academic settings and in everyday life. From baking to budgeting, fractions are everywhere, making their understanding and application universally valuable.



.png)
.png)
.png)




