What Is The Square Root?

Introduction to Square Roots

Square roots may sound like a tricky concept at first, but once you understand the basics, they’re much simpler than you think. The square root of a number is a value that, when multiplied by itself, gives the original number. It’s a fundamental mathematical concept with real-world applications in many fields, from geometry to engineering, construction, and even physics.

Imagine you're drawing a square on a piece of paper for a school project, and you know the area of the square is 25 cm². To figure out how long each side of the square needs to be, you’d use the square root. Since the square root of 25 is 5, you know each side of your square should be 5 cm long – pretty useful, right? Whether you're working with shapes or solving problems in everyday life, square roots are an essential tool.

Key Terms and Definitions

• Square Number: This is the result of multiplying a number by itself. For example, when you multiply 4 by 4, you get 16 – so 16 is a square number.
• Square Root (√): The square root of a number is the value that, when multiplied by itself, gives the original number. For example, the square root of 9 is 3, because 3 × 3 = 9. When you write it in maths, it will be written as √9 = 3.
• Perfect Squares: These are numbers that have an exact whole number as their square root. For example, 16 is a perfect square because its square root is a whole number (√16 = 4).
• Non-perfect Squares: These are numbers that don’t have a whole number as their square root. For instance, the square root of 20 is not a whole number, so 20 is a non-perfect square. The square root of 20 is approximately 4.47.
• Radical Symbol (√): This is the symbol used to represent the square root. For example, √25 means "the square root of 25."

By understanding these terms, you’re well on your way to mastering square roots!

Step-by-Step Guide to Calculating Square Roots

Now that we’ve covered the basics, let’s walk through how to calculate square roots, starting with perfect squares. These are numbers that have whole numbers as their square roots.

1. Identify the number you want to find the square root of: First, take note of the number you are working with.
2. Think of a number that multiplies by itself to give the original number: The square root of a number is the value that, when multiplied by itself, results in that original number.
3. Check your answer by squaring it: Once you think you’ve found the correct square root, multiply it by itself to ensure you’ve got the right answer.

It’s important to realise that finding the square root of a number doesn’t have to involve typical calculation, or working something out. For perfect squares, finding the square root is more about recognising patterns and remembering key numbers, which is why knowing square numbers is so important since it’s simply doing the same thing in reverse.

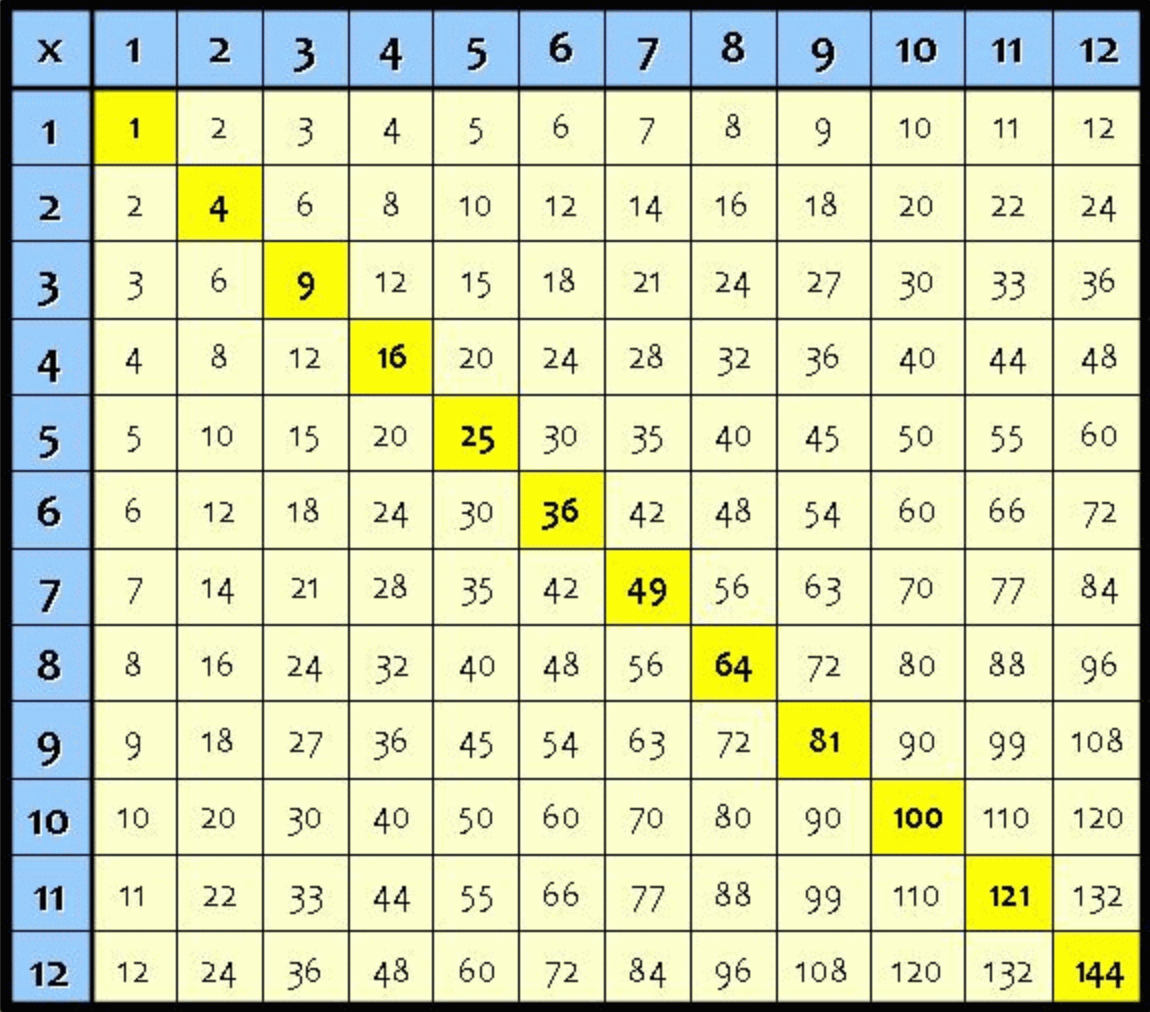
It could be handy to use a times table chart to help you identify those patterns, like this one here. As you can see, 36 is highlighted in yellow as a perfect square, and you can see (as we saw in the example) it aligns with 6 and 6 if you look up and across on the grid. Understanding and remembering these patterns will make finding the square root much easier!

Square Roots of Non-Perfect Squares

Not all numbers are as simple as perfect squares, like 4 or 25, which have neat whole numbers as their square roots. Numbers like 20 or 50, known as non-perfect squares, don’t have an exact whole number as their square root. Instead, their square roots result in long decimal numbers, which is why we often need to approximate them. Don’t worry, we’ll look at using a calculator for accuracy later too.

Approximating Square Roots of Non-Perfect Squares

To approximate the square root of a non-perfect square, the goal is to find the two closest perfect squares between which the number falls. For example, if you’re trying to approximate √20:

1. Identify the closest perfect squares: In this case, √16 = 4 and √25 = 5. Since 20 lies between 16 and 25, you know that √20 will be somewhere between 4 and 5.
2. Estimate more closely: Since 20 is closer to 16 than 25, you can estimate that √20 is slightly more than 4. A rough guess might be around 4.47.

Using a Calculator for Precision

While approximation is useful, sometimes you’ll need an exact value, especially for non-perfect squares. This is where a calculator comes in handy. By using the square root function (√), you can find the precise square root in just a few seconds. For example, typing 50 into a calculator and pressing the √ button gives you 7.071, confirming that the square root is just over 7. Give it a go now!

Practise Problems

Now that you’ve learnt how to calculate square roots, it’s time to put your skills to the test! Start with some simpler perfect squares and then move on to estimating non-perfect squares. If you have a calculator, you can check the actual answer and see how close your estimation was.

1. What is the square root of 49?
2. What is √64?
3. What is √100?
4. Approximate the square root of 20.
5. Approximate the square root of 45.
6. Calculate the exact value of √75.

Answers

1. √49 = 7
   • Explanation: Since 7 × 7 = 49, the square root of 49 is 7.
2. √64 = 8
   • Explanation: 8 × 8 = 64, so the square root of 64 is 8.
3. √100 = 10
   • Explanation: 10 × 10 = 100, so the square root of 100 is 10.
4. √20 = 4.47
   • Explanation: √20 is between √16 = 4 and √25 = 5. Since 20 is closer to 16 but almost halfway in between, the square root is approximately 4.47.
5. √45 = 6.71
   • Explanation: √45 falls between √36 = 6 and √49 = 7. Estimating, it’s a bit closer to 7, so √45 is approximately 6.71.
6. √75 = 8.66
   • Explanation: Entering √75 into your calculator will give the exact value, so the answer is 8.66 (to 2 decimal places).

Mastering square roots is all about understanding the relationship between squaring and square roots, and practicing both perfect and non-perfect squares. With a bit of repetition, you’ll find yourself calculating square roots with ease, whether it’s in maths problems or everyday life.